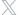Many investors know that geographic diversification can improve investment returns without increasing risk. But how much to invest abroad, if anything, is subject to heated debate. Some investment advisors recommend that U.S. investors put up to one-third of their stock portfolio in foreign stocks. Others argue that political uncertainties and currency fluctuations make the value of foreign investments far more volatile than domestic, that this volatility is not offset by higher returns, and that diversification benefits are not sufficient to offset this disadvantage. They point out that U.S. investors can get overseas exposure by investing in the stocks of domestic companies such as IBM and Coca-Cola, which derive a large portion of their revenue from overseas operations.

In an attempt to settle debates such as these, modern portfolio theory, pioneered by Harry Markowitz in the 1950s, uses optimization techniques and historical statistics to construct the portfolio with the lowest risk for a given level of return. This theory, which requires lots of data and number crunching, has found practical application among pension funds and other institutional investors over the past 20 years. With the advent of cheap computing power and the Internet, commercial services are beginning to bring portfolio optimization to individual investors participating in 401(k) plans.

But while portfolio optimization has been enormously useful in clarifying our thinking about investment decisions and providing broad guidelines about how much to invest overseas, its specific recommendations are highly sensitive to the way returns are measured. We still have no substitute for human judgment about how to blend data from the past with our expectations about the future.

THE OPTIMAL GLOBAL PORTFOLIO

Investors desire high investment returns and they also wish to minimize risk; thus, a riskier security must have a higher expected return to compensate investors for assuming the additional risk. In constructing a portfolio, investors are faced with the problem of allocating their money among various assets, including domestic and foreign equities and corporate and government bonds - and making this trade-off between risk and return. An "efficient portfolio” provides the highest expected (mean) return for a given level of risk (standard deviation). Portfolio optimization can be thought of as identifying all such "efficient portfolios” that result from the changing blend of various assets in the portfolio. The investor can then choose among them, depending on his or her tolerance for risk.

One thing that portfolio theory made clear was that the risk of a portfolio depends not only on the volatility of the individual assets that constitute it, but also on their correlations - the extent to which the asset returns "move up and down together.” Correlations can range between negative one (completely negatively correlated) and positive one (completely positively correlated); a value of zero means the returns are completely unrelated to one another. The lower the correlation among asset returns in a portfolio - other things equal - the lower is the risk of that portfolio. That is how diversification can reduce risk.

Consider the recent record of five broad classes of assets an index of U.S. stocks, an index of European stocks, an index of Pacific stocks, an index of government/corporate bonds, and a typical U.S. money market investment. Between January 1980 and September 1998, the U.S. stock fund had the highest annualized returns, at 15.5 percent; the U.S. money market fund had the lowest risk, with a standard deviation of less than 1 percent (see tables below).

To figure the optimal portfolio, however, we also need to look at the correlations between the returns. We see that the U.S. money market fund was negatively correlated with the stock funds during this period, reflecting the fact that high interest rates generally occur along with low stock prices. The various stock markets exhibited similar movements during this period, and this is reflected in their positive correlations.

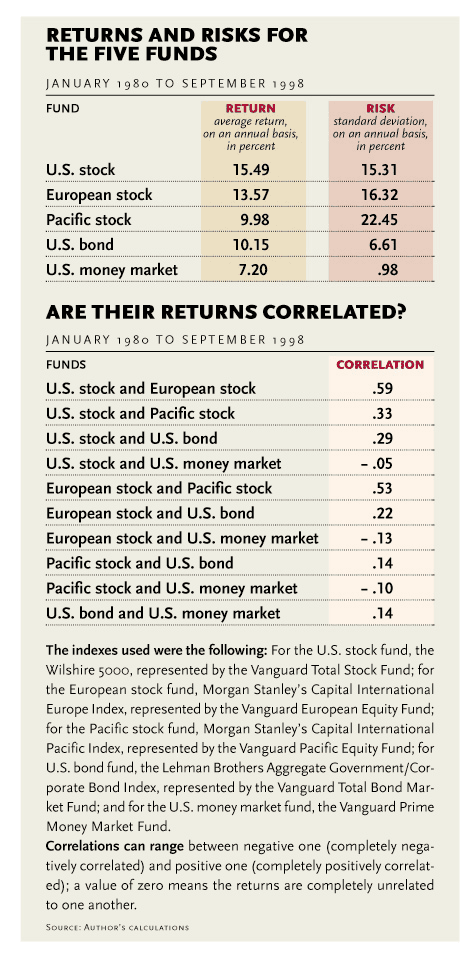
Portfolio optimization techniques allow us to find the blend of the five assets that minimize the standard deviation of the portfolio's return for any given level of expected return. We show five of these optimal portfolios based on data for the five funds. (We assume no short selling.) The least risky portfolio invests 99 percent of its assets in the U.S. money market fund and 1 percent in the European stock fund; U.S. stocks and bonds are not included. The riskiest portfolio is fully invested in U.S. stocks. The moderate risk portfolio has a "conventional” asset allocation, with 51 percent in U.S. stocks, 42 percent in U.S. bonds, and 7 percent in European stocks.

Perhaps the most striking feature is the complete exclusion of the Pacific stock fund from all of the portfolios. Looking at the history of returns and risk, it is easy to see why. During the period in question, it was the most volatile with the highest standard deviation, at 22 percent. This greatly exceeded the volatility of the next riskiest fund, the European stock fund, with a standard deviation of 16 percent. Despite its high risk, the Pacific stock fund also had low returns; the returns for the U.S. and European stock funds and the U.S. bond fund exceeded it. Since the returns on the Pacific fund were also positively correlated with these three funds, the benefits of diversification it could have provided were too small to offset its own poor performance. For similar reasons, the European stock fund, while not excluded altogether, is a relatively small part of the optimal portfolios; it also had a lower return and higher risk than the U.S. stock fund, and its returns were positively correlated with U.S. stocks, thus offering limited benefits through diversification.

STABILITY AND THE PRACTICAL LIMITATIONS TO PORTFOLIO THEORY

Using this procedure to make investment decisions makes sense only if asset volatility and correlations are stable over time. In fact, volatilities can change; they can "swing” from high to low values. One could simply assume that the most recent data are the most relevant, and ignore observations from the distant past. But, as a rule, more data are better than less, and ignoring available data decreases the reliability of estimates.

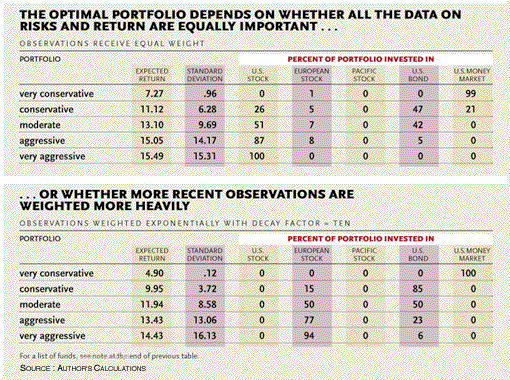
One alternative approach is to use exponential weights. Instead of applying the same weight to each data point, as done when calculating a simple average, the exponential average places relatively more weight on the more recent observations. Portfolio theory, however, leaves us with no obvious way to choose the speed with which the observations decline in importance. Picking a decay factor of ten, for example, means that the weight given to an observation declines by half after approximately ten observations.

When we refigure the optimal portfolios using a decay factor of ten, the results diverge significantly from the previous calculations. The most surprising difference the complete exclusion of U.S. stocks, as well as Pacific stocks. With the exception of the most conservative portfolio, which is completely invested in the U.S. money market, the portfolios include only U.S. bonds and European stocks. Recall that the earlier portfolios included a very small proportion of European stocks. This dramatic difference is due solely to the weighting scheme that placed more emphasis on recent observations.

This pinpoints a fundamental limitation of portfolio optimization. It also explains why, despite widespread acceptance, the theory has proved to be a challenge as a practical guide in real-life investment decisions - such as how much to invest in foreign stocks - even for professional money managers and sophisticated institutional investors. At the very least, investors must still decide how to incorporate past information into expectations about the future.

One expects (hopes?) that investors base their decisions on the fundamentals of global economic conditions and how those fundamentals are likely to affect asset returns. So whether and how much they should commit to overseas investments will depend, in the end, on each investor's view of the future economic prospects of the various geographic regions relative to the domestic economy.

Portfolio optimization is simply a computational convenience that helps the investor translate his or her views of the future asset returns, risks, and correlations into the portfolio that best represents this view. It does not replace the informed judgment that is the ultimate arbiter of investment decisions.

Katerina Simons is an Economist in the Research Department of the Federal Reserve Bank of Boston. Her article, "Should U.S. Investors Invest Overseas?” appeared in the November/December 1999 issue of the New England Economic Review.